Корень 2450

14 декабря 2012

Довольно часто при решении задач мы сталкиваемся с большими числами, из которых надо извлечь квадратный корень. Многие ученики решают, что это ошибка, и начинают перерешивать весь пример. Ни в коем случае нельзя так поступать! На то есть две причины:

1. Корни из больших чисел действительно встречаются в задачах. Особенно в текстовых;
2. Существует алгоритм, с помощью которого эти корни считаются почти устно.

Этот алгоритм мы сегодня и рассмотрим. Возможно, какие-то вещи покажутся вам непонятными. Но если вы внимательно отнесетесь к этому уроку, то получите мощнейшее оружие против квадратных корней.

Итак, алгоритм:

1. Ограничить искомый корень сверху и снизу числами, кратными 10. Таким образом, мы сократим диапазон поиска до 10 чисел;
2. Из этих 10 чисел отсеять те, которые точно не могут быть корнями. В результате останутся 1—2 числа;
3. Возвести эти 1—2 числа в квадрат. То из них, квадрат которого равен исходному числу, и будет корнем.

Прежде чем применять этот алгоритм работает на практике, давайте посмотрим на каждый отдельный шаг.

Ограничение корней

В первую очередь надо выяснить, между какими числами расположен наш корень. Очень желательно, чтобы числа были кратны десяти:

102 = 100;
202 = 400;
302 = 900;
402 = 1600;
…
902 = 8100;
1002 = 10 000.

Получим ряд чисел:

100; 400; 900; 1600; 2500; 3600; 4900; 6400; 8100; 10 000.

Что нам дают эти числа? Все просто: мы получаем границы. Возьмем, например, число 1296. Оно лежит между 900 и 1600. Следовательно, его корень не может быть меньше 30 и больше 40:

То же самое — с любым другим числом, из которого можно найти квадратный корень. Например, 3364:

Таким образом, вместо непонятного числа мы получаем вполне конкретный диапазон, в котором лежит исходный корень. Чтобы еще больше сузить область поиска, переходим ко второму шагу.

Отсев заведомо лишних чисел

Итак, у нас есть 10 чисел — кандидатов на корень. Мы получили их очень быстро, без сложных размышлений и умножений в столбик. Пора двигаться дальше.

Не поверите, но сейчас мы сократим количество чисел-кандидатов до двух — и снова без каких-либо сложных вычислений! Достаточно знать специальное правило. Вот оно:

Последняя цифра квадрата зависит только от последней цифры исходного числа.

Другими словами, достаточно взглянуть на последнюю цифру квадрата — и мы сразу поймем, на что заканчивается исходное число.

Существует всего 10 цифр, которые могут стоять на последнем месте. Попробуем выяснить, во что они превращаются при возведении в квадрат. Взгляните на таблицу:

1	2	3	4	5	6	7	8	9	0
1	4	9	6	5	6	9	4	1	0

Эта таблица — еще один шаг на пути к вычислению корня. Как видите, цифры во второй строке оказались симметричными относительно пятерки. Например:

22 = 4;
82 = 64 → 4.

Как видите, последняя цифра в обоих случаях одинакова. А это значит, что, например, корень из 3364 обязательно заканчивается на 2 или на 8. С другой стороны, мы помним ограничение из предыдущего пункта. Получаем:

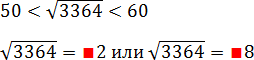
Красные квадраты показывают, что мы пока не знаем этой цифры. Но ведь корень лежит в пределах от 50 до 60, на котором есть только два числа, оканчивающихся на 2 и 8:

Вот и все! Из всех возможных корней мы оставили всего два варианта! И это в самом тяжелом случае, ведь последняя цифра может быть 5 или 0. И тогда останется единственный кандидат в корни!

Финальные вычисления

Итак, у нас осталось 2 числа-кандидата. Как узнать, какое из них является корнем? Ответ очевиден: возвести оба числа в квадрат. То, которое в квадрате даст исходное число, и будет корнем.

Например, для числа 3364 мы нашли два числа-кандидата: 52 и 58. Возведем их в квадрат:

522 = (50 +2)2 = 2500 + 2 · 50 · 2 + 4 = 2704;
582 = (60 − 2)2 = 3600 − 2 · 60 · 2 + 4 = 3364.

Вот и все! Получилось, что корень равен 58! При этом, чтобы упростить вычисления, я воспользовался формулой квадратов суммы и разности. Благодаря чему даже не пришлось умножать числа в столбик! Это еще один уровень оптимизации вычислений, но, разумеется, совершенно не обязательный 🙂

Примеры вычисления корней

Теория — это, конечно, хорошо. Но давайте проверим ее на практике.

Задача. Вычислите квадратный корень:

Для начала выясним, между какими числами лежит число 576:

400 < 576 < 900
202 < 576 < 302

Теперь смотрим на последнюю цифру. Она равна 6. Когда это происходит? Только если корень заканчивается на 4 или 6. Получаем два числа:

24; 26.

Осталось возвести каждое число в квадрат и сравнить с исходным:

242 = (20 + 4)2 = 576

Отлично! Первый же квадрат оказался равен исходному числу. Значит, это и есть корень.

Задача. Вычислите квадратный корень:

Здесь и далее я буду писать только основные шаги. Итак, ограничиваем число:

900 < 1369 < 1600;
302 < 1369 < 402;

Смотрим на последнюю цифру:

1369 → 9;
33; 37.

Возводим в квадрат:

332 = (30 + 3)2 = 900 + 2 · 30 · 3 + 9 = 1089 ≠ 1369;
372 = (40 − 3)2 = 1600 − 2 · 40 · 3 + 9 = 1369.

Вот и ответ: 37.

Задача. Вычислите квадратный корень:

Ограничиваем число:

2500 < 2704 < 3600;
502 < 2704 < 602;

Смотрим на последнюю цифру:

2704 → 4;
52; 58.

Возводим в квадрат:

522 = (50 + 2)2 = 2500 + 2 · 50 · 2 + 4 = 2704;

Получили ответ: 52. Второе число возводить в квадрат уже не потребуется.

Задача. Вычислите квадратный корень:

Ограничиваем число:

3600 < 4225 < 4900;
602 < 4225 < 702;

Смотрим на последнюю цифру:

4225 → 5;

Как видим, после второго шага остался лишь один вариант: 65. Это и есть искомый корень. Но давайте все-таки возведем его в квадрат и проверим:

652 = (60 + 5)2 = 3600 + 2 · 60 · 5 + 25 = 4225;

Все правильно. Записываем ответ.

Заключение

Многие спрашивают: зачем вообще считать такие корни? Не лучше ли взять калькулятор и не парить себе мозг?

Увы, не лучше. Давайте разберемся в причинах. Их две:

• На любом нормальном экзамене по математике, будь то ГИА или ЕГЭ, пользоваться калькуляторами запрещено. И за пронесенный в класс калькулятор могут запросто выгнать с экзамена.
• Не уподобляйтесь тупым американцам. Которые не то что корни — они два простых числа сложить не могут. А при виде дробей у них вообще начинается истерика.

В общем, учитесь считать. И все будет хорошо. Удачи!

Транскрипт

1 МКУ «Закаменское районное управление образования» МБОУ «Холтосонская СОШ» Школьная научно-практическая конференция «Первые шаги» Номинация: математика Способы извлечения квадратного корня из многозначных чисел. Попова Алена, 6 класс МБОУ «Холтосонская СОШ», 6класс Домашний адрес: РБ, Закаменский район, село Холтосон, ул. Комсомольская, дом 41 Контактный телефон: Руководитель: Харакшинова Ирина Вячеславовна Год выполнения:

2 Оглавление Введение История квадратного корня.4 2. Методы извлечение квадратного корня Разложение подкоренного выражения на простые множители Извлечение квадратного корня уголком Методика быстрого извлечения квадратного корня.7 Выводы…9 Список литературы

3 Введение. Можно ли представить себе мир без чисел? Без чисел ни покупки не сделаешь, ни времени не узнаешь, ни номера телефона не наберёшь. А космические корабли, лазеры и все другие технические достижения? Они были бы попросту невозможны, если бы не наука о числах. В наш век высоких технологий и повсеместного использования компьютера умение быстро и правильно производить сложные вычисления ни в коем случае не утратило своей актуальности. Гибкость ума является предметом гордости людей, а способность, например, быстро производить вычисления вызывает откровенное удивление. Такие навыки помогут человеку в учебе, в быту, в профессиональной деятельности. Кроме того, быстрый счет — настоящая гимнастика для ума, приучающая в самых сложных жизненных ситуациях находить в кратчайшее время хорошие и нестандартные решения. В этом году я случайно услышала, «излечение квадратного корня». Мне стало интересно, что же такое квадратный корень и как его извлечь? Если ли алгоритмы для извлечения квадратного корня? С этим вопросом я обратилась к своей учительнице математики, она ответила, что такие алгоритмы есть, и посоветовала мне самой исследовать этот вопрос. Я заинтересовалась и решила изучить этот вопрос глубже, чем он освещен в школьной программе. В работе представлены простые алгоритмы извлечения квадратного корня, которыми может овладеть каждый. Цель работы: Исследовать различные способы вычисления квадратных корней. Задачи: 1. Проанализировать математическую литературу по данной теме, использовать также интернет-ресурсы. 2. Составить алгоритмы по вычислению квадратного корня в случаях его вычисления «нацело». 3. Привести примеры быстрого извлечения квадратного корня. 3

4 Глава 1.История квадратного корня. Потребность в действиях возведения в степень и извлечения корня была вызвана, как и другие четыре арифметических действия, практической жизнью. Так, наряду с задачей вычисления площади квадрата, сторона которого а известна, с давних пор встречалась обратная задача: «Какую длину должна иметь сторона квадрата, чтобы его площадь равнялась в?» Применяемый знак корня произошел от обозначения, которое применяли немецкие математики в.в., называвшие алгебру «Косс», а алгебраистами «косстистами». Неизвестные числа с 17 века стали обозначать последними буквами латинского алфавита x, y, z. Однако долго ещё неизвестное в уравнении писали буквой R (от «Radix» — «корень»), а квадрат его буквой q («quadratus»). Это объяснение не является общепринятым. В самых старых рукописях перед числом, из которого нужно извлечь корень, ставилась точка, а позднее точка или узкий ромбик с черточкой, направленной вправо и вверх. Так образовался знак. S Зная время t, можно найти путь 4, 9t 2. Решим обратную задачу. при свободном падении по формуле: Задача. Сколько секунд будет падать камень, сброшенный с высоты 122,5 м? 2 Решение: Чтобы найти ответ, нужно решить уравнение 4, 9t 122, 5. Из него находим, что t Теперь осталось найти такое положительное число t, что его квадрат равняется 25. Этим числом является 5, так как Значит, камень будет падать 5 с. Искать положительное число по его квадрату приходится и при решении других задач, например при отыскании длины стороны квадрата по его площади. Введем следующее определение: Определение. Неотрицательное число, квадрат которого равен неотрицательному числу а, называется квадратным корнем из а. Это число обозначают а. Таким образом ( а) 2 а и а 0. Пример. Так как , 1 1, 2 4, 3 9, то 0 0, 1 1, 4 2, 9 3. Из отрицательных чисел нельзя извлекать квадратные корни, так как квадрат любого числа или положителен, или равен нулю. Например, выражение числового значения. 25 не имеет В записи а знак называют знаком радикала (от латинского «радикс» — корень), а число а — подкоренным числом. Например, в записи 25 подкоренное число 4

5 n. равно 25. Так как ( 10 ) n, 2 n n то Это означает, что квадратный корень из числа, записанного единицей и 2n нулями, равен числу, записываемому единицей и n нулями: n нулей n нулей Во время работы над данным исследованием мною была обнаружена интересная информация. Оказывается, существует неофициальный праздник, посвященный квадратному корню. День квадратного корня -праздник, отмечаемый девять раз в столетие: в день, когда и число, и порядковый номер месяца являются квадратными корнями из двух последних цифр года (например, 2 февраля 2004 года: ). Впервые этот праздник отмечался 9 сентября 1981 года ( ). Основателем праздника является школьный учитель Рон Гордон из города Редвуд Сити, Калифорния, США. По состоянию на 2010год Гордон продолжает публиковать заметки о придуманном им празднике, активно контактируя поэтому поводу со СМИ. Главным блюдом на этом «праздничном столе» обычно являются вареные кубики из овощей и выпечка в форме математического знака квадратного корня По объективным математическим причинам этот праздник может отмечаться строго девять раз в столетие (семь раз в первой половине века и дважды во второй), всегда в одни и те же дни: 1 января хх01 года 2 февраля хх04 года 3 марта хх09 года 4 апреля хх16 года 5 мая хх25 года 6 июня хх36 года 7 июля хх49 года 8 августа хх64 года 9 сентября хх81 года При этом интересно заметить, что промежуток (в годах) между праздниками составляет непрерывную последовательность нечётных чисел: 3, 5, 7 и т. д. 5

6 Глава II. Методы извлечения квадратного корня Первый способ — таблица квадратов, телефоны и калькуляторы, можно воспользовались ими, но если их нет под рукой Разложение подкоренного выражения на множители. Второй способ разложение подкоренного выражения на множители. Например, найдем.число 6561 делится на 3. Разложим 6561 на множители: 6561= =81 81, Извлечение квадратного корня уголком. Третий способ. Извлечение квадратного корня уголком. 1-й шаг. Число 8649 разбиваем на грани справа налево; каждая из которых должна содержать две цифры. Получаем две грани:. 2-й шаг. Извлекаем квадратный корень из первой грани 86, получаем с недостатком. Цифра 9 это первая цифра корня. 3-й шаг. Число 9 возводим в квадрат (9 2 = 81) и число 81 вычитаем из первой грани, получаем 86-81=5. Число 5 первый остаток. 4-й шаг. К остатку 5 приписываем вторую грань 49, получаем число й шаг. Удваиваем первую цифру корня 9 и, записывая слева, получаем-18 К числу нужно приписать такую наибольшую цифру, чтобы произведение числа, которое мы получим, на эту цифру было бы либо равно числу 549, либо меньше, чем 549. Это цифра 3. Она находится путем подбора: количество десятков числа 549, то есть число 54 делится на 18, получаем 3, так как = 549. Цифра 3 это вторая цифра корня. 6-й шаг. Находим остаток = 0. Так как остаток равен нулю, то мы получили точное значение корня 93. Пример: Для поверки мы возвысили в квадрат 63 и к результату приложили 113; так как в сумме получилось данное число 4082, то действие сделано верно. 6

7 2.3. Методика быстрого извлечения квадратного корня 1= = = =4 2 и т.д. Пример: найдём 529 Решение: 1)_ )_ )_ )_ )_ )_ )_ )_ )_ )_ )_ )_408 7

8 27 13)_ )_ )_ )_ )_ )_ )_ )_ )_ )_ )_ Ответ: 529 = 23 8

9 Выводы. Извлечение квадратного корня часто встречается в заданиях школьного курса математики, при подготовке к экзаменам, в практических вычислениях в быту. В работе представлены простые алгоритмы извлечения арифметических корней, которыми может овладеть каждый. Описанные в работе методы извлечения корней встречаются во многих источниках. Тем не менее, разобраться в них оказалось для меня непростой задачей, что вызвало немалый интерес. Представленные алгоритмы позволят всем, кто заинтересуется данной темой, быстрее овладеть навыками вычисления квадратного корня, их можно использовать при проверке своего решения и не зависеть от наличия в кармане калькулятора. Тем более, что на экзамене в 9 и 11 классах применение калькулятора не допускается. Работая над проектом, я пришла к следующим выводам: Для извлечения квадратного корня существуют таблицы квадратов. Для двухзначных чисел, можно разложить число на простые множители и извлечь квадратный корень из произведения. Таблицы квадратов бывает недостаточно, извлечение корня разложением на множители — трудоёмкая задача, которая тоже не всегда приводит к желаемому результату. Я постаралась найти способы, которые бы позволили извлечь квадратный корень. Привела примеры быстрого извлечения квадратного корня. В рамках данного проекта исследовались алгоритмы извлечения арифметического корня, которые позволят всем, кто заинтересуется данной темой, быстрее овладеть навыками вычисления квадратного корня, и применить их при решении задач и экзаменационных работ, независимо от наличия в кармане калькулятора. 9