Построение перпендикуляра к прямой

Прямая, плоскость, их уравнения

Эта статья о составлении уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой. Сначала даны необходимые теоретические сведения, далее приведены подробные решения характерных примеров, в которых требуется записать уравнение прямой, проходящей через заданную точку перпендикулярно заданной прямой.

Принцип составления уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой.

Прежде чем приступить к нахождению уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой, обговорим некоторые важные моменты.

В средней школе на уроках геометрии доказывается следующая теорема: через заданную точку плоскости можно провести единственную прямую, перпендикулярную заданной прямой. Однако, через заданную точку трехмерного пространства можно провести бесконечно много прямых, перпендикулярных заданной прямой. Действительно, если построить плоскость , проходящую через заданную точку M1 перпендикулярно к заданной прямой b, то любая прямая, лежащая в этой плоскости и проходящая через заданную точку M1, перпендикулярна заданной прямой b.

Таким образом, задача о составлении уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой, имеет практическое значение лишь для случая на плоскости.

В трехмерном пространстве обычно ищут уравнение плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.

Итак, пусть на плоскости зафиксирована прямоугольная декартова система координат Oxyz, задана прямая b, которой в этой системе координат соответствует уравнение прямой на плоскости некоторого вида, задана точка , и требуется написать уравнение прямой a, проходящей через точку M1 перпендикулярно прямой b.

Обсудим способы решения этой задачи.

Из условия нам известны координаты точки М1, лежащей на прямой a, уравнение которой нам предстоит составить. Но этого мало. Чтобы написать уравнение прямой a, нам нужно знать еще или координаты направляющего вектора прямой a, или координаты нормального вектора прямой a, или угловой коэффициент прямой a. Откуда нам получить эти данные? Ответ очевиден — из заданного уравнения прямой b. Так как прямые b и a перпендикулярны по условию, то направляющий вектор прямой b является нормальным вектором прямой a, нормальный вектор прямой b является направляющим вектором прямой a, а угловые коэффициенты и прямых b и a соответственно связаны соотношением (это мы обсуждали в статье перпендикулярные прямые, перпендикулярность прямых).

Итак, пусть мы нашли направляющий вектор прямой b вида , тогда нормальным вектором прямой a является вектор , где , следовательно, мы можем записать общее уравнение прямой a, которая проходит через точку и имеет нормальный вектор , в виде .

Если мы определили нормальный вектор прямой b вида , то направляющий вектор прямой a есть вектор , где , следовательно, мы можем составить каноническое уравнение прямой a или параметрические уравнения прямой a, которая проходит через точку и имеет направляющий вектор , в виде или соответственно.

Если же мы нашли угловой коэффициент прямой b, то угловой коэффициент прямой a равен , следовательно, мы можем написать уравнение прямой a, проходящей через точку и имеющей угловой коэффициент , в виде (об этом написано в статье уравнение прямой с угловым коэффициентом).

От найденного уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой, можно при необходимости перейти к другому виду уравнения этой прямой.

Решение примеров на составление уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой.

Давайте разберем составление уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой, на примерах.

Пример.

Напишите уравнение прямой a, которая в прямоугольной системе координат Oxy на плоскости проходит через точку и перпендикулярна прямой b, заданной каноническим уравнением прямой .

Решение.

Очевидно, что — направляющий вектор прямой . Так как прямая a перпендикулярна прямой b, то координаты вектора являются координатами нормального вектора прямой a, то есть, . Уравнение прямой, проходящей через точку и имеющей нормальный вектор , записывается в виде . Это и есть искомое уравнение прямой, проходящей через точку перпендикулярно прямой .

Ответ:

Пример.

Составьте уравнение прямой, проходящей через начало прямоугольной декартовой системы координат Oxy перпендикулярно прямой .

Решение.

Очевидно, — нормальный вектор прямой , тогда — направляющий вектор прямой, уравнение которой мы ищем. Запишем уравнение прямой, которая проходит через начало координат (точку ) и имеет направляющий вектор : . Это и есть уравнение прямой, проходящей через начало координат перпендикулярно прямой .

Ответ:

Пример.

Напишите уравнение прямой, проходящей через точку перпендикулярно прямой .

Решение.

Угловой коэффициент прямой равен , тогда угловой коэффициент прямой, которая ей перпендикулярна, равен . Следовательно, уравнение прямой, проходящей через точку перпендикулярно прямой , имеет вид .

Ответ:

Список литературы.

Некогда разбираться?

Закажите решение

Примеры:

1. Даны прямая и точка на ней. Построить прямую проходящую через данную точку и перпендикулярную к данной прямой.

Дано: прямая m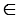, Mm.

Построить: МPm.

Решение:

Произвольно строим с помощью линейки прямую m и отмечаем на ней точку М.

На лучах прямой m, исходящих из точки М, с помощью циркуля откладываем равные отрезки МА и МВ (МА = МВ). Для этого строим окружность с центром в точке М, при этом всю окружность строить не обязательно, достаточно сделать пометки по разные стороны от точки М (смотри выделенное красным).

Затем строим две окружности с центрами в точках А и В радиуса АВ (полностью окружности строить необязательно, смотри выделенное фиолетовым и красным цветом).

Данные окружности пересекаются в двух точках, обозначим их Р и Q. Проведем с помощью линейки через точку М и одну из точек Р или Q прямую, например, МР.

Докажем, что прямая МР — искомая прямая, т.е. что МPm.

Рассмотрим треугольник АРВ.

АР = ВР, т.к. по построению это радиусы одинаковых окружностей, следовательно, АРВ — равнобедренный. По построению МА = МВ, т.е. МР — медиана равнобедренного треугольника, тогда по свойству равнобедренного треугольника МР и высота, т.е. МPm. Что и требовалось доказать.

2. Даны прямая и точка не лежащая на этой прямой. Построить прямую проходящую через данную точку и перпендикулярную к данной прямой.

Дано: прямая m, Mm.

Построить: МNm.

Решение:

Произвольно строим с помощью линейки прямую m и отмечаем точку М, не лежащую на прямой m.

Далее строим окружность с центром в данной точке М, пересекающую прямую m в двух точках, которые обозначим буквами А и В (всю окружность строить необязательно, смотри выделенное красным цветом).

Затем построим две окружности с центрами в точках А и В, проходящие через точку М (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Эти окружности пересекутся в точке М и еще в одной точке, которую обозначим буквой N. Проведем прямую МN.

Докажем что, прямая МN — искомая, т.е. МNm.

Гипермаркет знаний>>Математика>>Математика 7 класс. Полные уроки>>Геометрия: Построение перпендикулярной прямой. Полные уроки

ТЕМА УРОКА: Построение перпендикулярной прямой.

Цели урока:

• Познакомить учащихся с определением перпендикулярных прямых и их свойствах;
• Формирование умений анализировать изученный материал и навыков применения его для решения задач;
• Показать значимость изучаемых понятий;
• Развитие познавательной активности и самостоятельности получения знаний;
• Воспитание интереса к предмету, чувства прекрасного.

Задачи урока:

• Формировать навыки в построении перпендикулярной прямой с помощью масштабной линейки, циркуля чертежного треугольника.
• Проверить умение учащихся решать задачи.

План урока:

• Проверка усвоения, изученного материала.
• Изучение нового материала.
• Построение перпендикулярной прямой.

Проверка усвоения, изученного материала.

Найдите ошибку:

• Два угла называются смежными, если у них одна сторона общая, а другие стороны являются дополнительными прямыми.
• Сумма смежных сторон равна 180?.
• Если два угла равны, то совместные с ними углы равны.
• Если угол не развёрнутый, то его градусная мера больше 180?.
• Угол, смежный с прямым углом, есть прямой угол.
• Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами сторон другого.
• Вертикальные углы различны.
• Если прямые пересекаются, значит, они перпендикулярны.
• Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной который имеет одним из своих концов их общую точку.
• Биссектрисой угла называется отрезок, который проходит из вершины треугольника, проходит межу его лучами и делит угол пополам.

Изучение нового материала.

Изучая геометрические фигуры, вы уже не раз встречались с перпендикулярными прямыми. Например, смежные стороны прямоугольника перпендикулярны. Как убедиться в том, что две линии (прямые) перпендикулярны? С древних пор строители проверяли перпендикулярность стены основанию дома с помощью отвеса, то есть грузика на веревке. Отсюда и произошло название перпендикуляра: латинское «перпендикулярис” означает «отвесной”. Чтобы построить перпендикуляр к прямой, достаточно построить прямой угол. Это вы умеете делать с помощью чертежного треугольника и с помощью транспортира.

Итак, давайте выясним, какие прямые называют перпендикулярными.

Файл:O.gif Определение.

Две прямые, пересекающиеся под прямым углом, называются перпендикулярными. (рис.2)

Файл:T.gif Теорема.

Через каждую точку прямой можно провести перпендикулярную ей прямую, и только одну.

Доказательство.

Пусть а — данная прямая и А — данная точка на ней. Обозначим через ах одну из полупрямых прямой а с начальной точкой А (рис. 3). Отложим от полупрямой а1 угол (a1b1), равный 90°.
Тогда прямая, содержащая луч b1, будет перпендикулярна прямой а.

Как вы думаете, отрезки могут быть перпендикулярными?

Да. Вообще, можно назвать перпендикулярными любые две линии, лежащие на перпендикулярных прямых. Какие же еще геометрические фигуры могут быть перпендикулярными?
Варианты ответов: луч и отрезок, два луча, отрезок и прямая и т.д. Отрезки (или лучи), лежащие на перпендикулярных прямых, так же называют перпендикулярными отрезками (или лучами).
Про перпендикулярные линии часто говорят, что каждая из них – «перпендикуляр» к другой. В математике слово «перпендикулярные” обозначают знаком ┴. Если при пересечении двух прямых образуется один прямой угол, то и три остальных угла тоже будут прямыми.

Итак, перпендикулярными называются две прямые, при пересечении которых образуется четыре прямых угла.
Пришло время научиться стоить перпендикулярные прямые. И начнем мы с построение перпендикулярной прямой через точку, лежащую на данной прямой и не лежит на прямой.

Рассмотрим эти два случая с подробным описанием.

Построение перпендикулярной прямой.

Через точку O провести прямую, перпендикулярную данной прямой a.

Возможно два варианта:

1. точка O лежит на прямой a;
2. точка О не лежит на прямой a.

Рассмотрим поочередно оба варианта.

Первый вариант.

Шаг 1. Проводим окружность с произвольным радиусом r с центром в точке O. Окружность пересекает прямую в точках A и B.

Шаг 2. Из точек A и B проводим окружности с радиусом AB. Пусть тоска С – точка пересечения этих окружностей.

Обращаю ваше внимание на то что точки А и В мы получили на первом шаге, при построении окружности с произвольным радиусом.

Шаг 3. Искомая прямая проходит через точки С и О.

Доказательство.

Как было уже сказано выше все четыре угла образованных при пересечении двух прямых перпендикулярны если хотя бы один из них перпендикулярен, т.е. является прямым и равен 90 градусов.

Второй вариант такой же простой только имеет немного другой принцип поиска наших начальных точек А и В.

Второй вариант.

Шаг 1. Из точки O проводим окружность некоторым радиусом r, таким чтобы окружность пересекала прямую a. Пусть A и B – точки пересечения окружности с прямой a.

Шаг 2. Проведем окружности тем же радиусом r с центрами в точках A и B. Пусть точка O1 – точка пресечения этих окружностей, лежащая в полуплоскости, отличной от той, в которой лежит точка O.

Шаг 3. Проведем через точки O и O1 прямую. Это и будет искомая прямая.

Доказательство.

Пусть прямые OO1 и AB пересекаются в точке С. Δ AOB = Δ BO1A по третьему признаку равенства треугольников (AO = OB = AO1 = O1B, по построению, AB – общая). Отсюда следует, что ∠ OAС = ∠ O1AC. Δ OAC = Δ O1AC по первому признаку равенства треугольников (AO = AO1, по построению, ∠ OAС = ∠ O1AC, AС – общая). Следовательно ∠ OСA = ∠ O1CA, а так как эти углы смежные, то они прямые. Поэтому OC – перпендикуляр, опущенный из точки O на прямую a.

Т. е. с помощью циркуля и линейки мы можем стоить перпендикулярные прямые, независимо от того точка через какую должен проходить перпендикуляр находиться на отрезке или за его пределами. Оба варианта имеют три шага, единственная сложность в том что бы правильно найти начальные точки А и В.

Интересный факт:

Теорема о двух милиционерах.

В математике есть много интересных возможно даже забавных или смешных теорем какие на первый взгляд не представляя собой ничего серьезного. Но на самом деле несут смысл в некоторых разделах или ответвлениях науки, так же могут быть выведенными специально для доказательства других теорем или просто быть случайно доказанными. Некоторые математические законы называют по аналогии с ситуациями в реальной жизни. В мировой математики есть очень интересная теорема с не менее интересным названием «Теорема о двух милиционерах».

Теорема о двух милиционерах это теорема в математическом анализе о существовании предела у функции, которая «зажата» между двумя другими функциями, имеющими одинаковый предел.

Название теоремы происходит из того факта, что если два милиционера держат между собой преступника и при этом идут в камеру, то заключённый также вынужден туда идти. В разных странах эта теорема называется по разному. Теорема сжатия, теорема о двух карабинерах, теорема о сэндвиче (или правило сэндвича), теорема о трёх струнах, теорема о двух жандармах, теорема о двух городовых.

Вопросы:

1. Сформулируйте определение окружности и круга?
2. Какая разница между диаметром и радиусом?
3. Какие прямые называются перпендикулярными?
4. Какой угол между перпендикулярными прямыми?
5. Чем пользуються для построения перпендикулярных прямых?

Список использованных источников:

1. Урок на тему «Наглядная геометрия» Самылина Марина Валентиновна., г. Киев
2. «Единый государственный экзамен 2006. Математика. Учебно-тренировочные материалы для подготовки учащихся/ Рособрнадзор, ИСОП – М.: Интеллект-Центр, 2006»
3. Мазур К. И. «Решение основных конкурсных задач по математике сборника под редакцией М. И. Сканави»
4. Прямая в пространстве, справочник математических формул «Прикладная математика»
5. Прямая на плоскости, справочник математических формул «Прикладная математика»
6. Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина «Геометрия, 7 – 9: учебник для общеобразовательных учреждений»

Над уроком работали:

Самылина М.В.

Потурнак С.А.

Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на Образовательном форуме, где на международном уровне собирается образовательный совет свежей мысли и действия. Создав блог, Вы не только повысите свой статус, как компетентного преподавателя, а и сделаете весомый вклад в развитие школы будущего. Гильдия Лидеров Образования открывает двери для специалистов высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.

Предмети > Математика > Математика 7 класс

Г Л А В А I.

ОСНОВНЫЕ ПОНЯТИЯ.

§ 10. ПЕРПЕНДИКУЛЯР К ПРЯМОЙ.
ПОСТРОЕНИЕ ПЕРПЕНДИКУЛЯРА К ПРЯМОЙ

1. Перпендикуляр к прямой.
Основные свойства перпендикуляра.

Прямые линии, образующие между собой прямые углы, называются взаимно перпендикулярными.

Прямые АВ и СD (черт. 54) взаимно перпендикулярны.

Перпендикулярность прямых обозначается знаком _|_. На чертежах 53 и 54 АВ_|_DС и DС _|_ АВ.

Каждая из этих прямых называется перпендикуляром к другой. АВ — перпендикуляр к СD, и СD — перпендикуляр к АВ.

К данной прямой через данную на ней точку можно провести, только один перпендикуляр (черт. 55).

В самом деле, если АВ_|_СD, то всякая другая прямая, проведённая через точку О прямой СD, например LК, не будет перпендикулярна к ней, так как углы КОС и КОD не будут прямыми углами, а один из них будет больше прямого угла, другой меньше.

Точно так же можно провести только один перпендикуляр к данной прямой АВ через точку О и в том случае, когда точка О лежит не на прямой АВ, а вне её (черт. 56).

Если ОС_|_АВ, то всякая другая прямая, проходящая через точку О, уже не будет перпендикулярна к прямой АВ. Доказательство этого утверждения будет дано позднее.

2. Построение перпендикуляра к прямой.

Для вычерчивания прямых углов употребляется угольник, или чертёжный треугольник (черт. 57). Прямой угол может быть изображён в любом положении (черт. 58).

Проведение перпендикуляра к данной прямой А В с помощью чертёжного треугольника через точку О, данную на самой прямой АВ, показано на чертеже 59.

На чертеже 60 показано проведение перпендикуляра к прямой АВ через точку О, данную вне этой прямой.

3. Проверка чертёжного треугольника.

Чтобы проверить чертёжный треугольник, надо начертить прямую линию, взять на ней какую-нибудь точку и, приняв луч за сторону угла, построить при помощи треугольника прямой угол с вершиной в данной точке. Затем чертёжный треугольник надо перевернуть, приложить той же стороной прямого угла к этой прямой в противоположном направлении от вершины и построить второй прямой угол с вершиной в той же точке. Если начерченные прямые совпадут (черт. 61), то чертёжный треугольник верен, если же не совпадут, то треугольник не верен (черт. 62).

4. Углы острый и тупой. Углы, большие развёрнутого.

Так как все прямые углы равны между собой, то прямой угол может быть принят за меру углов.

Угол, меньший прямого, называется острым углом (черт. 63).

Угол, больший прямого, но меньший развёрнутого, называется тупым (черт. 64).

Могут быть углы и большие развёрнутого (черт. 65). Однако мы ограничимся рассмотрением только тех углов, которые меньше развёрнутого; углы же, большие развёрнутого, мы рассматривать не будем, кроме тех случаев, когда это будет особо оговорено.

5. Эккер.

Для построения прямых углов на земной поверхности применяется особый прибор, который называется эккером.

Эккер представляет собой два бруска, укреплённых под прямым углом. На концах брусков ставятся булавки или тонкие гвозди так, чтобы прямые, соединяющие их (черт. 66), были взаимно перпендикулярны. Эккер укрепляется на треножнике или на палке.

Чтобы построить на земле прямой угол, надо наметить вершину угла, а эккер поместить так, чтобы точка пересечения взаимно перпендикулярных прямых (на чертеже они изображены пунктиром) оказалась на одной отвесной линии с намеченной вершиной угла на местности. Затем по направлению булавок одного бруска провешить одну прямую линию, а по направлению булавок второго бруска — вторую прямую (черт. 67).

Если надо провести прямую, перпендикулярную к данной прямой в данной точке, то эккер ставится над этой точкой так, чтобы направление булавок одного бруска совпадало с направлением данной прямой. Затем по направлению другого бруска провешивается вторая прямая, которая с данной прямой образует прямой угол, т. е. перпендикулярна к ней.

Упражнения.

1. Начертить прямую, взять на ней точку и провести с помощью чертёжного треугольника перпендикуляр к данной прямой через данную точку.

2. Начертить прямую, взять точку вне этой прямой и с помощью чертёжного треугольника провести к прямой перпендикуляр, проходящий через данную точку.

3. Назвать все углы, которые имеются на чертежах 68 и 69 (не считая углов, которые больше развёрнутого).

4. Вырезать из плотной бумаги квадрат. Разрезать его на две равные части, как показано на чертеже 70, и из полученных двух фигур составить фигуры, изображённые на чертеже 71, а, б, в, г, д, е, ж, э.